机器学习

机器学习就是自动找函数式

1. 
2. 要问自己想要找什么样的函数，先去创建一个任务，regression和classification
3. 
4. 不能只会做判断输出1、2，后面发展到需要generate生成有结构的东西
5. 
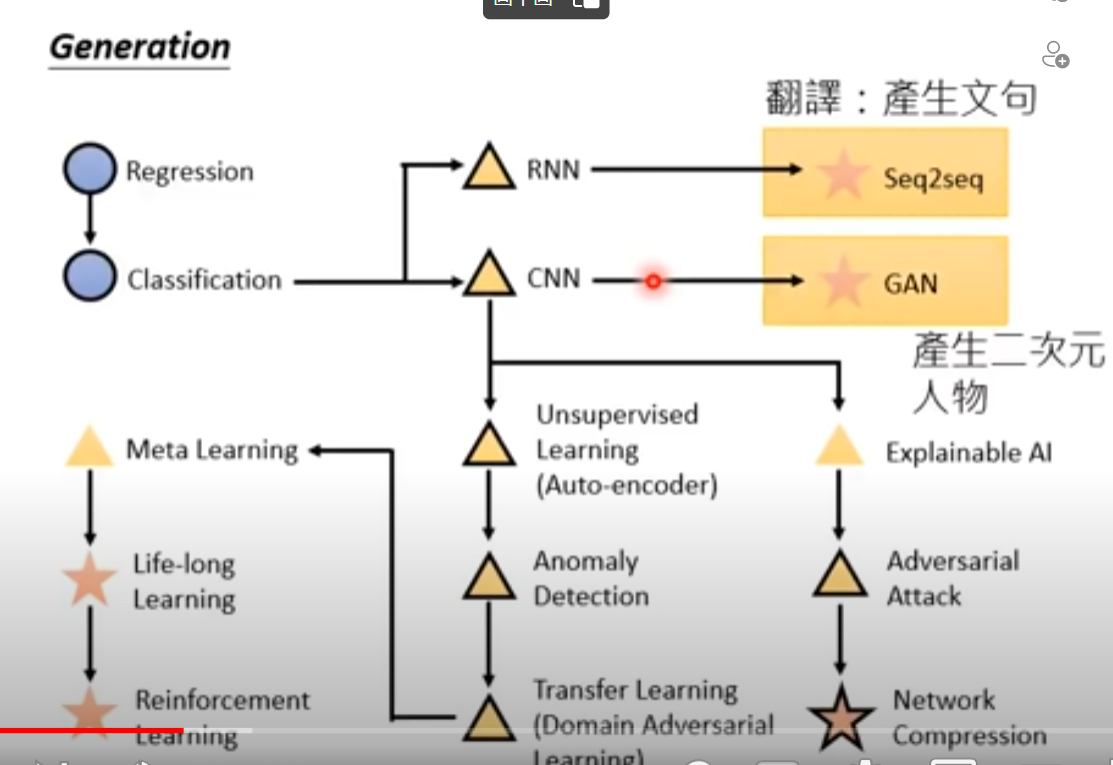
6. 怎么告诉机器想要找什么样子的函数：supervised learning,而这需要labeled data，即标注数据集，即告诉机器想要得到的结果是什么样子
7. 
8. 评估一个函数的好坏：函数的LOSS
9. 下一步，期待机器会自动找出LOSS最低的函数
10. 
11. 机器如何找到你想要的函数：Linear->Network Architecture：给机器一个函数寻找的范围

Supervised learning vs Reinforcement learning

1. 
2. Supervised learning:监督学习，给数据需要标注
3. Reinforcement learning:强化学习，给的数据不需要标注

Meta Learning = learn to learn 让机器学会学习

1. 
2. 

life-long-learning

1. 终身学习
2. 

Regression

1. 找函数

2. 

   三步走

   1. 第一步，找一个model
   2. 
   3. 第二步，定义function set，在function set中找到一个LOSS值最低的function
   4. 
   5. goodness of function,判断此函数的LOSS值，如何判断：找一个关于此函数的函数，能判断此函数的LOSS值的函数，输入值为a function,输出值为how bad it is,能判断此函数的好坏的值
   6. 假设函数是：
   7. 
   8. 对此函数的结果求方差（其中^y是求得的估计值，减去的是每一只宝可梦的实际值带入得到的值）
   9. 
   10. 第三步，找到最好的function
   11. 找一个function，使得找到的L(f)最小，f* = argL(f)
   12. 或者找到一个w*,b*，使得argmin L(w,b)最小
   13. 第四步，Gradient Descent，目的是找到可以使LOSS值最小的w

       Gradient Descent

       1. 暴力的做法是穷举所有的w,找到LOSS值最小的w

       2. 可以：随机选取初始的w0；构建横轴为w，纵轴为L的坐标系，在初始的w位置L对w的导数（切线斜率），如果切线斜率为负数，则随着w的增大，LOSS值减小，所以要增加w的值；如果斜率为正，则要减小w的值$\frac{dL}{dw}|w=w0$

       3. 增加/减小w的值应该有多大：1. 取决于dL/dw的值（切线斜率、导数）有多大，如果越大，越陡峭，移动距离就越大 2.取决于learning rate的值的大小（事先定好的一个常数），如果learning rate的值较大，踏出一步的时候，参数更新的幅度就比较大，则学习的效率、速度就比较快

       4. $w1 = w0 - \eta*\frac{dL}{dw}|w=w0$

       5. $w2 = w0 - \eta*\frac{dL}{dw}|w=w0$

       6. 经过多次iteration（迭代）之后就到达了local optimal(局部最优解)，此时在local optimal的点，算出的微分都是0了，不会再进行更新

       7. 

       8. 当是两个参数时，$w*,b* = arg minL(w,b)$

       9. 思路相同，先选取两个初始值，w0和b0

       10. 然后在初始值位置求偏导$\frac{\partial L}{\partial w}|w=w0,b=b0$,$\frac{\partial L}{\partial b}|w=w0,b=b0$

       11. 更新，$w1 = w0 - \eta*\frac{\partial L}{\partial w}|w=w0,b=b0$,$b1 = b0 - \eta\frac{\partial L}{\partial b}|w=w0,b=b0$

       12. 进行多次iteration(迭代),就可以到达local optimal

       13. 因为Regression是线性的，所以单调，local optimal == global optimal

       14. 

       15. gradient指的是$\frac{\partial L}{\partial w}$,$\frac{\partial L}{\partial b}$所组成的一个vector(向量)，且gradient的符号是倒三角$\nabla$

       16. 

       17. 

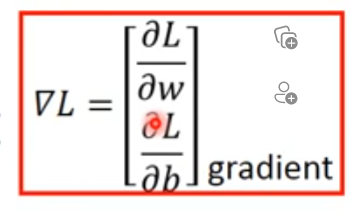
       18. 二维可视化：$(-\eta\frac{\partial L}{\partial b},-\eta\frac{\partial L}{\partial w})$的方向是切线的法线方向，指向的是圆心

       19. local optimal == global optimal的问题：因为linear regression(线性回归)的loss值是convex（凸面）的，所以没有local optimal(局部最优解)

       20. 

       21. 

       22. 求复合函数的偏导：外面导里面不导 * 里面导